We use the formula for the relativistic Doppler effect:
$\begin{align*}\lambda = \lambda_0 \sqrt{\frac{c \pm v}{c \mp v}}\end{align*}$
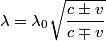We choose the upper signs because the wavelength has increased: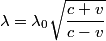
$\begin{align*}\lambda = \lambda_0 \sqrt{\frac{c + v}{c - v}}\end{align*}$
The increase in wavelength also means that the astronomical object is moving away from the earth. We now solve for v: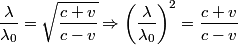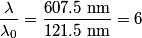
$\begin{align*}\frac{\lambda}{\lambda_0} = \sqrt{\frac{c + v}{c - v}} \Rightarrow \left( \frac{\lambda}{\lambda_0}\right)^2 = ...$
$\begin{align*}\frac{\lambda}{\lambda_0} = \frac{607.5 \mbox{ nm}}{121.5 \mbox{ nm}} = 6\end{align*}$
Therefore,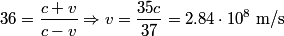
$\begin{align*}36 = \frac{c + v}{c - v} \Rightarrow v = \frac{35 c}{37} = 2.84 \cdot 10^{8} \mbox{ m/s}\end{align*}$
Therefore, answer (D) is correct.

Solution to 2001 Problem 71